二元函数的极限与连续ppt课件2020最新免费版

编辑点评：二元函数的极限与连续ppt课件

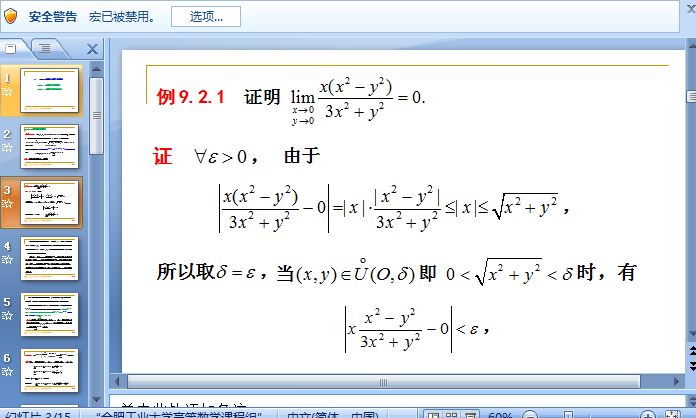
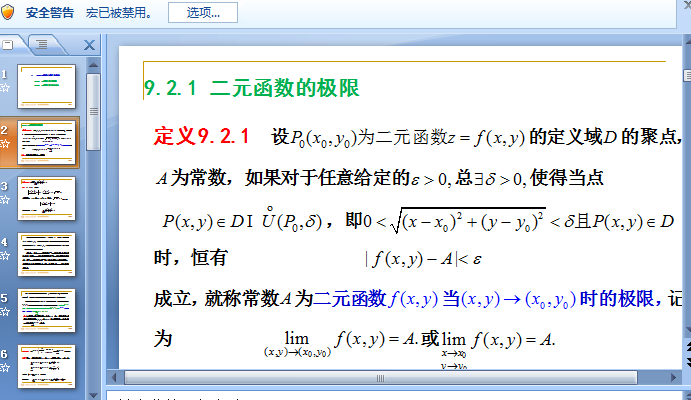
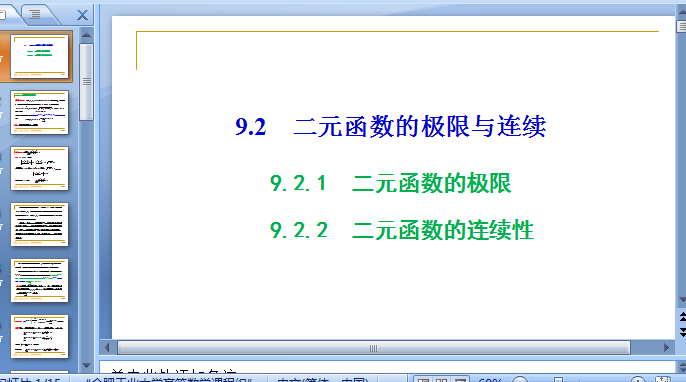
函数在数学上是是一个必学的知识点之一，那么小编为大家准备了相应的ppt课程资料供大家下载使用，无论老师 还是学生都会有帮助的，二元函数的极限与连续性与一元函数的极限相类似,二元函数的极限同样是二元函数微积分的基础，快来下载吧

二次元函数的基本方式

二次元公式只含有一个未知数，并且未知数项的最高次数是2的整式bai方程叫做一元二次方程。它的标准形式为:ax2+bx+c=0（a≠0）。

一元二次方程有5种解法，即直接开平方法、配方法、公式法、因式分解法、图象法。

公式法不能解没有实数根的方程（也就是b2-4ac<0的方程），其它所有一元二次方程都能解。

因式分解法，必须要把所有的项移到等号左边，并且等号左边能够分解因式，使等号右边化为0。

配方法比较简单：首先将二次项系数a化为1，然后把常数项移到等号的右边，最后在等号两边同时加上一次项系数绝对值一半的平方，左边配成完全平方式，再开方就得解了。

数学公式是人们在研究自然界物与物之间时发现的一些联系，并通过一定的方式表达出来的一种表达方法。

学好数学并不是靠死记硬背 住数学公式去套上用，而是要靠理解 ，你不理解怎么都学不好 。学好数学没有捷径，要靠平时多做题，每做一道题总结一次是什么类型，有什么解题思路。

函数ppt预览

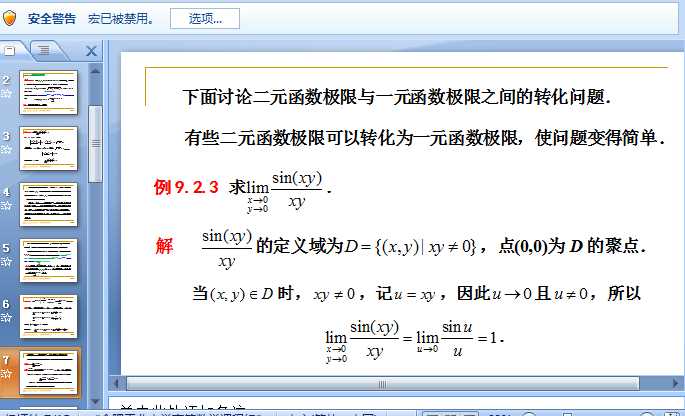
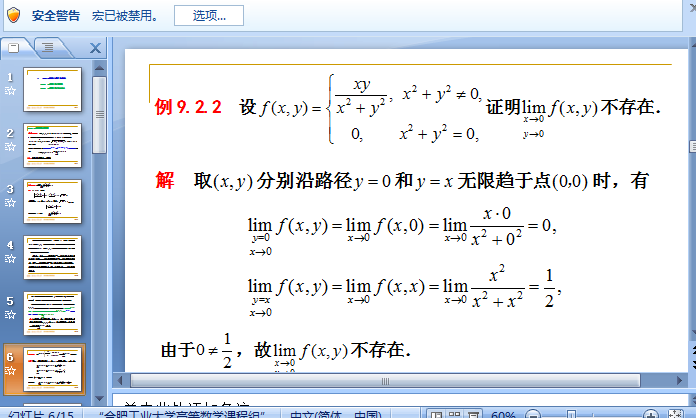
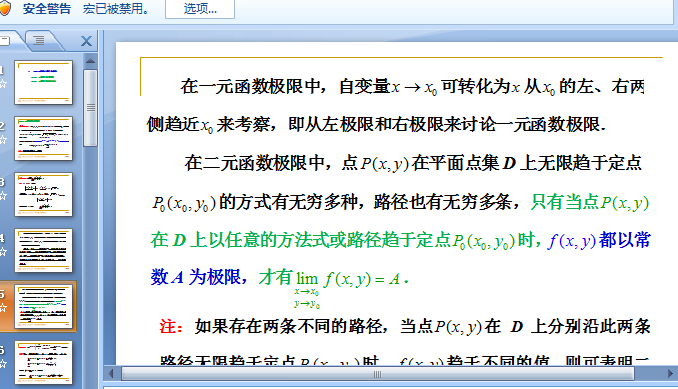
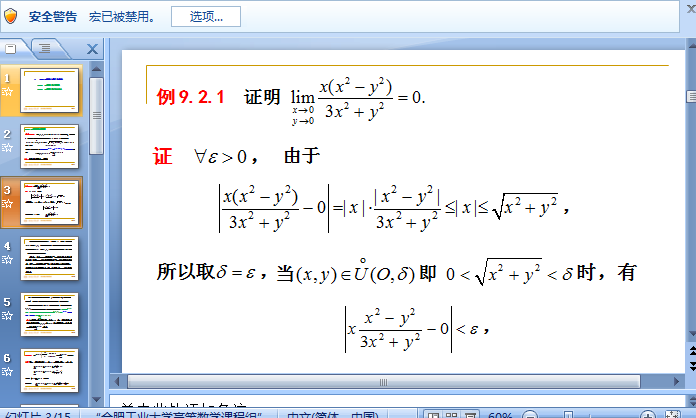
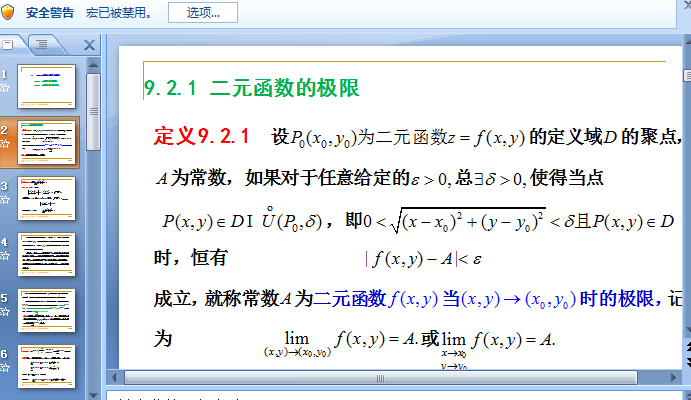
二元一次方程的解法

方程两边都是整式,含有两个未知数，并且含有未知数的项的次数都是1的方程，叫做二元一次方程.使方程左右两边相等的未知数的值叫做方程的解

你能区分这些方程吗？

（二元一次方程）；

（一元一次方程）；

(一元二次方程）；

（二元二次方程）。

对二元一次方程概念的理解应注意以下几点：

①等号两边的代数式是否是整式；

②在方程中“元”是指未知数，‘二元’是指方程中含有两个未知数；

③未知数的项的次数都是1，实际上是指方程中最高次项的次数为1，在此可与多项式的次数进行比较理解，切不可理解为两个未知数的次数都是1.

使二元一次方程两边相等的一组未知数的值，叫做二元一次方程的一个解.

对二元一次方程的解的理解应注意以下几点：

①一般地，一个二元一次方程的解有无数个，且每一个解都是指一对数值，而不是指单独的一个未知数的值；

②二元一次方程的一个解是指使方程左右两边相等的一对未知数的值；反过来，如果一组数值能使二元一次方程左右两边相等，那么这一组数值就是方程的解；

③在求二元一次方程的解时，通常的做法是用一个未知数把另一个未知数表示出来，然后给定这个未知数一个值，相应地得到另一个未知数的值，这样可求得二元一次方程的一个解.

注意点

（1）二元一次方程组：含有两个未知数的两个一次方程所组成的一组方程，叫做二元一次方程组。 [1] 

（2）二元一次方程组的解：二元一次方程组中两个方程的公共解，叫做二元一次方程组的解.

对二元一次方程组的理解应注意：

①方程组各方程中，相同的字母必须代表同一数量，否则不能将两个方程合在一起.

②怎样检验一组数值是不是某个二元一次方程组的解，常用的方法如下：将这组数值分别代入方程组中的每个方程，只有当这组数值满足其中的所有方程时，才能说这组数值是此方程组的解，否则，如果这组数值不满足其中任一个方程，那么它就不是此方程组的解.

常用解法

代入消元法

（1）概念：将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来，代入另一个方程中，消去一个未知数，得到一个一元一次方程，最后求得方程组的解. 这种解方程组的方法叫做代入消元法，简称代入法.

（2）代入法解二元一次方程组的步骤

①选取一个系数较简单的二元一次方程变形，用含有一个未知数的代数式表示另一个未知数；

②将变形后的方程代入另一个方程中，消去一个未知数，得到一个一元一次方程（在代入时，要注意不能代入原方程，只能代入另一个没有变形的方程中，以达到消元的目的. ）；

③解这个一元一次方程，求出未知数的值；

④将求得的未知数的值代入①中变形后的方程中，

求出另一个未知数的值；

⑤用“{”联立两个未知数的值，就是方程组的解；

⑥最后检验（代入原方程组中进行检验，方程是否满足左边=右边）.

加减消元法

（1）概念：当方程中两个方程的某一未知数的系数相等或互为相反数时，把这两个方程的两边相加或相减来消去这个未知数，从而将二元一次方程化为一元一次方程，最后求得方程组的解，这种解方程组的方法叫做加减消元法，简称加减法.

（2）加减法解二元一次方程组的步骤

①利用等式的基本性质，将原方程组中某个未知数的系数化成相等或相反数的形式；

②再利用等式的基本性质将变形后的两个方程相加或相减，消去一个未知数，得到一个一元一次方程（一定要将方程的两边都乘以同一个数，切忌只乘以一边，然后若未知数系数相等则用减法，若未知数系数互为相反数，则用加法）；

③解这个一元一次方程，求出未知数的值；

④将求得的未知数的值代入原方程组中的任何一个方程中，

求出另一个未知数的值；

⑤用“{”联立两个未知数的值，就是方程组的解

⑥最后检验求得的结果是否正确（代入原方程组中进行检验，方程是否满足左边=右边）。

函数的定义是什么

函数有很多定义，我从集论的定义答复你吧，这个定义很一般，也不给你抄定义的原文了，太长，你自己查一下集合论中的三个重要概念，它们是直积（笛卡尔积）、关系和映射，我只给你打个比方。

1）取一张坐标纸，定义X轴和Y轴。

2）坐标纸上的每个格子分别按照（x，y）标记，这种标记称为序偶。

3）由坐标纸上所有格子构成的集合称为直积，也就是由序偶构成的集合。

4）在坐标纸上随便倒一些染料，由被染色的格子构成的集合称为关系，即关系是直积的子集。

5）在坐标纸上画一条斜线，无论从左下到右上或从左上到右下，亦无论是直的或弯的。由被染色的格子构成的集合称为映射。相比于关系，映射强调单值性。

6）特殊情况：在坐标纸上画一个S型的曲线，由被染色的格子构成的集合称为一对多映射；画一条N型的曲线，由被染色的格子构成的集合称为多对一的映射。

7）映射是一般性的称谓，当直积由数集构成时，映射就称为函数；当直积由函数构成时，映射通常称为变换。

8）具体的例子如，人群的身高和体重分布是一种关系，车轮转的圈数和压过的路程是一个函数。