高斯课堂概率论与数理统计及答案pdf免费版

编辑点评：

让你4小时速成不挂科的蜂考高斯课堂的概率论与数理统计所配套的讲义，精品下载站附上最新高清无水印的高斯课堂概率论与数理统计及答案pdf免费下载，包含了14课时内容，需要的自己拿走不谢。

高斯课堂概率论与数理统计讲义预览

课程大纲

事件运算及概率

全概率、贝叶斯公式

一维随机变量

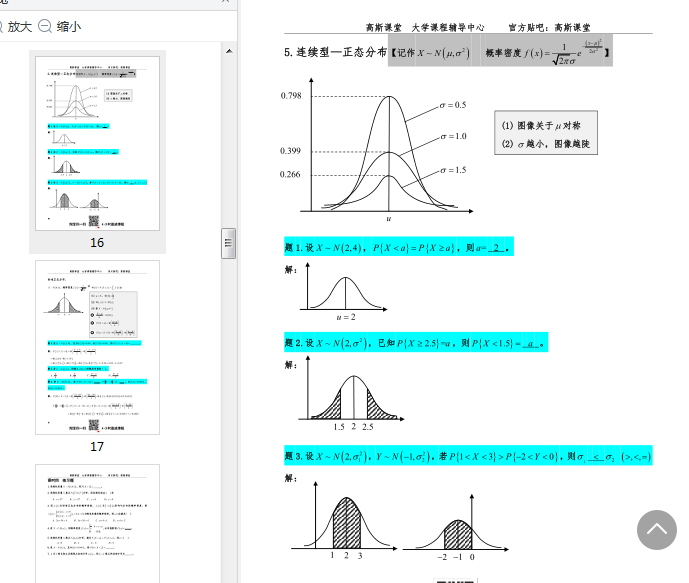
五种重要分布

二维离散型随机变量

二维连续型随机变量

E维连续型函数的分布

数学期望、方差、协方差

大数定理、中心极限定理

抽样分布

参数估计

置信区间

假设检验

二重积分（选学）

概率论与数理统计答案如下图

概率论与数理统计学习笔记分享

p1 绪论

p2 样本空间和随机事件

随机试验

在同样条件下重复进行

知道所有试验可能出现的结果

在实验室不知道这次会出现哪个结果

样本空间（集合）

随机试验所有可能的结果。

随机事件

样本空间的子集。
几个特殊的随机事件：

必然事件：一定会发生的事假。（比如把整个样本空间看做一个随机事件）

不可能事件：空集

基本事件：只包含一个样本点
例如：公交站现在有多少个人在等车？
样本空间：S={x : x>=0}
事件A表示等车人数大于等于0 A={x : x>=0} （必然事件）
事件A表示等车人数大于等于5 B={x : x>=5} (随机事件）
事件C表示恰好有三人等车 C={3} （基本事件）
事件D等车人数多于3且小于3 D={} （不可能事件）

p3 事件的相互关系和运算

关系

包含 A ⊂ B A\subset BA⊂B

相等 A=B

运算

和事件 A ∪ B A\cup BA∪B

积事件 A ∩ B A\cap BA∩B

逆事件A ￣ \overline AA

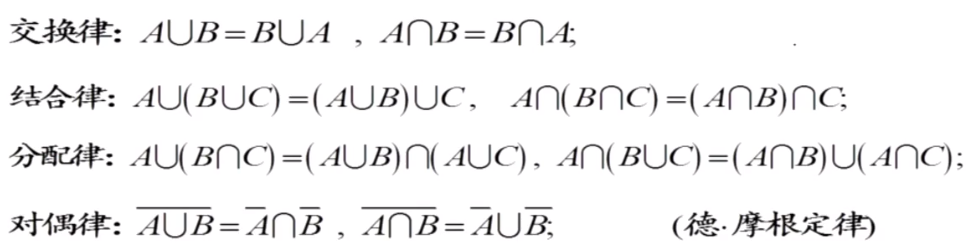
p4频率

随机事件A在N次随机实验中发生次数所占的比例，随着N增大趋于稳定。最终稳定到随机事件A发生的概率。

p5概率

讲到概率的的性质和一些简单的计算公式。

p6古典概型（等可能概型）

样本空间的样本点有限（有限性）

每个样本点出现概率相等（等可能性）

p7条件概率的定义

P ( B ∣ A ) P(B|A)P(B∣A) : A发生的情况下B发生的概率
P ( B ∣ A ) = P ( B A ) P ( A ) P(B|A)= \frac {P(BA)} {P(A)}P(B∣A)=P(A)P(BA)
后面包含了一些经典例题

p8条件概率

经典例题

p9全概率和贝叶斯公式

划分

样本空间S
第i事件A即为A i A_iAi
划分满足以下性质：

A 1 ∪ A 2 ∪ A 3 ∪ . . . . A n = S A_1\cup A_2\cup A_3 \cup....A_n=SA1∪A2∪A3∪....An=S

任意j,k满足A j ∩ A k = ϕ A_j \cap A_k=\phiAj∩Ak=ϕ

全概率公式

贝叶斯

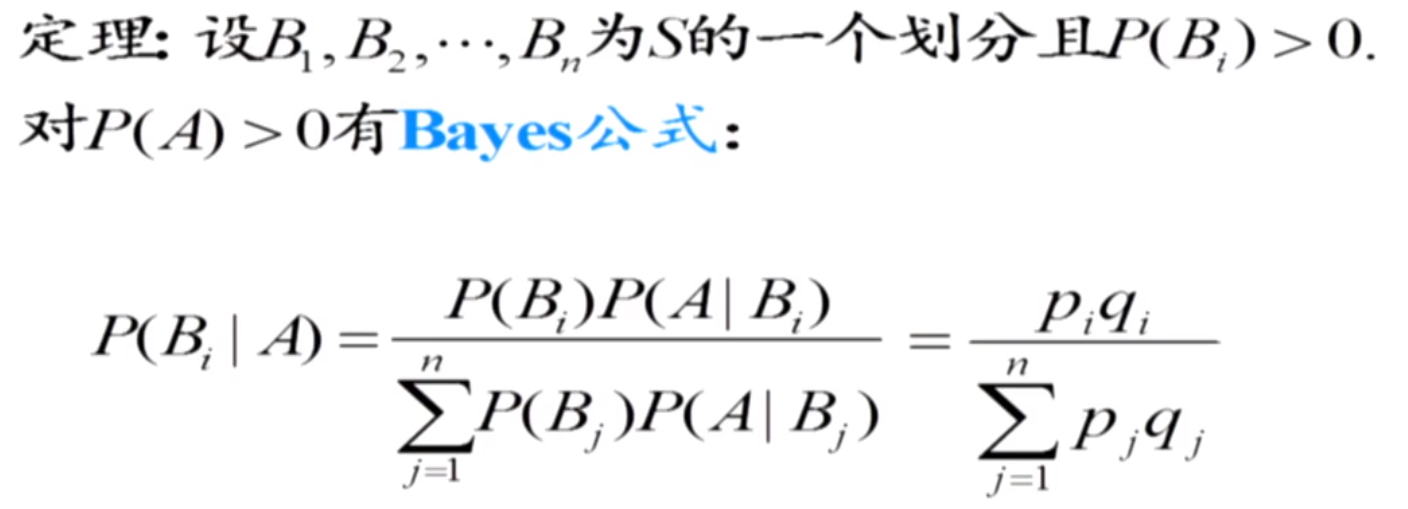
p10全概率和贝叶斯公式

例题讲解

p11事件的独立性

P ( A , B ) = P ( A ) ∗ P ( B ) P(A,B)=P(A)*P(B)P(A,B)=P(A)∗P(B)
独立和不相容两个概念，不相同。
独立性考虑的是A,B会不会相互影响
相容考虑的是两个事件有无交集

p12事件的独立性

经典例题

p13随机变量

随机变量实际上是一个函数：一个将样本点映射到实数空间的函数。方便我们描述随机数事件。

p14随机变量

分布

所有随机变量取值及其对应概率

p15离散随机变量的分布

二项分布（0-1分布）

二项分布记为：
X ～ 0 − 1 ( p ) X\sim 0-1(p)X～0−1(p) 发生概率为p
也可记为X ～ B ( 1 , p ) X\sim B(1,p)X～B(1,p) 也可表示进行一次伯努利实验，发生的概率为p
X ～ B ( n , p ) X\sim B(n,p)X～B(n,p)表示进行n次伯努利实验，发生的概率为p
例：抛一枚不均匀的硬币，正面向上概率为0.4
用X表示抛9次硬币正面向上的次数：
X服从二项分布X ～ B （ 9 ， 0.4 ） X \sim B（9，0.4）X～B（9，0.4）
用X表示抛9次硬币正面向上的次数：
X服从二项分布X ～ B （ 9 ， 0.6 ） X \sim B（9，0.6）X～B（9，0.6）
二项分布概率计算方法P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_n^k p^k{(1-p)}^{n-k}P(X=k)=Cnkpk(1−p)n−k

p16离散随机变量的分布

泊松分布

X ～ π ( λ ) 或 X ～ P ( λ ) X \sim \pi(\lambda) 或 X \sim P(\lambda)X～π(λ)或X～P(λ)
概率计算公式：
P ( x = k ) = λ k e − λ k ! P(x=k)=\frac{\lambda ^ke^{- \lambda}}{k!}P(x=k)=k!λke−λ

当n>10,p<0.1时泊松分布可看做二项分布的近似。概率计算结果基本一致。

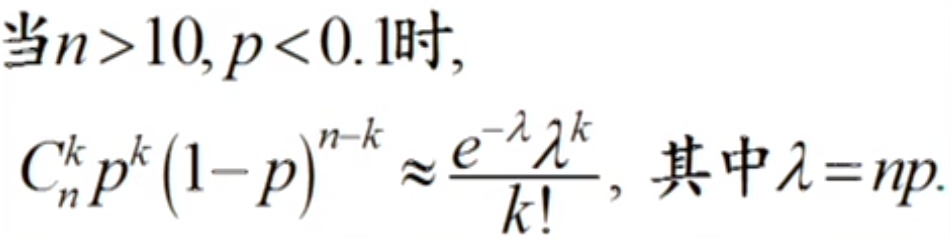
几何分布

几何分布记为：
x ～ G e o m ( p ) x \sim Geom(p)x～Geom(p)
概率计算公式：
P ( X = k ) = p ( 1 − p ) k − 1 P(X=k)=p{(1-p)}^{k-1}P(X=k)=p(1−p)k−1
典型服从几何分布例子：
我们投掷一枚骰子，6点向上时停止投掷。投掷的次数服从几何分布。

p17分布函数

（可以用来描述连续型和离散型随机变量的分布）
分布函数
F ( x ) = P （ X ≤ x ） 有 时 记 作 ： F X ( x ) = P （ X ≤ x ） F(x)=P（X\leq x）有时记作：F_X(x)=P（X\leq x）F(x)=P（X≤x）有时记作：FX(x)=P（X≤x）

p18分布函数

离散型随机变量分布和分布函数互推的例子

p19分布函数

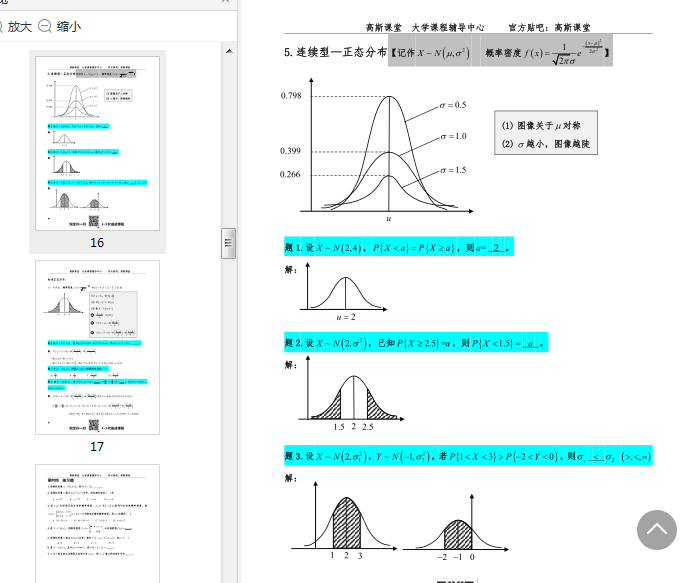
连续性随机变量的分布函数

p20 连续性随机概率密度函数

连续性变量才有概率密度函数

p21 连续性随机概率密度函数