高斯课堂复变函数与积分变换讲义笔记pdf免费版

编辑点评：

高斯课堂高数精品课程，复变函数与积分变换最新讲义免费分享，它适用大学期末考试/补考/重修/清考等人员，刷分还是考研，都是信手拈来，时间短，干货满满，重点已标记，你需要的都在这里。

课程大纲介绍

复数

复变函数

初等函数

级数

求积分

留数

利用留数求积分

Fourier傅里叶变换

Laplace拉普拉斯变换

映射（选学）

高斯课堂复变函数与积分变换图片预览

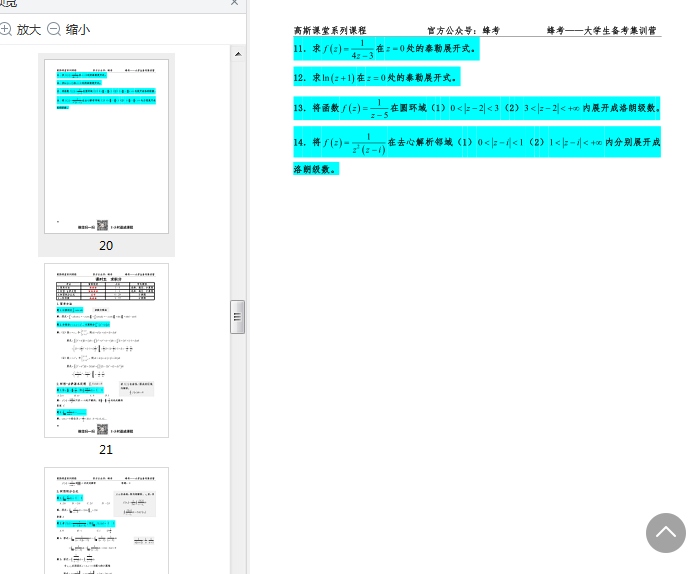
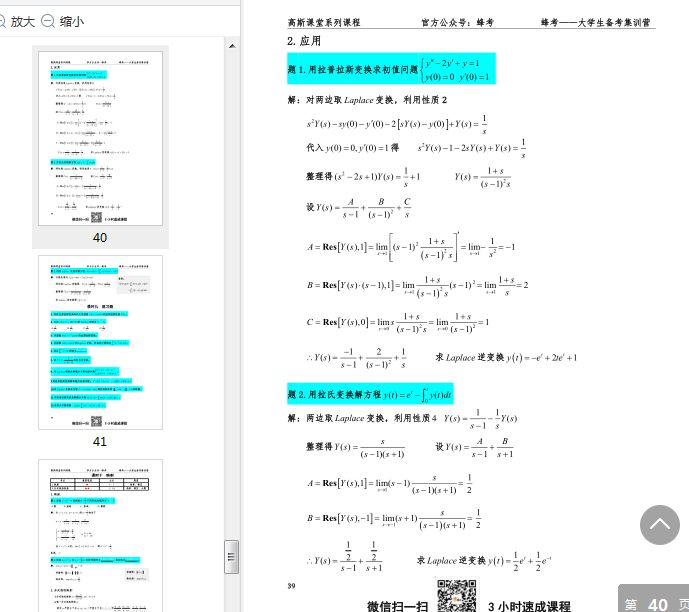
学习笔记整理

#复数及其运算

##复数的加减乘除

复数的基础知识相信大家在高中数学里已经学过了，需要注意的是复数的乘法和除法计算比较困难，大家可以多留心记一下。

##求复数的实部与虚部

这道题的复合函数求解较难，大家可以留意一下。

##求某复数的共轭复数

求一个复数的共轭复数，只需要将他的虚部的符号变一下（原来是正号，就变成负号，原来是负号，就变成正号），就行了。

##求模，辐角和辐角主值

这些公式中arg:argumentofacomplexnumber（复数的辐角）

###求模，辐角和辐角主值的例题

辐角主值的求法比较困难，需要在坐标上分别标出Re和Im的值，然后将他们对应的那个点与原点连接起来，所呈现出来的直线与Re轴正方向所成的夹角，就是辐角主值。

特别提醒，辐角主值的取值范围是-180°到180°

###又一道例题

##复数的开方

大家千万要注意，复数的开方与高中时实数的开方不一样，16开四次方不等于2，而需要用到专门的复数开方公式。在计算完成之后，记得加上K=0，1,2，3，……n-1;千万千万要记得，不是n,不是n,不是n,重要的事情说三遍。

##代数式，三角式，指数式转换。

重点知识整理

第一章：复数与复变函数

所谓复变函数，就是自变量为复数的函数。

研究主要对象是某种意义下可导的复变函数，称为解析函数。

知识点层次为：复数->复变函数->复变函数性质->初等解析函数及性质

复数代数式：z=x+iy

复数三角式：z=r(cosθ+isinθ)

欧拉公式：eiθ=cosθ+isinθ

指数式：z=reiθ

主值　：θ=argz=arctan(y/x)

棣莫弗公式：(cosθ+isinθ)n=cosnθ+isinnθ

解析函数

复变函数可导的条件：实部虚部两个二元函数可微，实部与虚部通过C-R条件联系起来。

若函数f(z)在z0某一领域处处可导，称f(z)在z0处解析。

若f(z)在区域E内每一点解析，称f(z)是E内的一个解析函数。

f在E内解析的充要条件是，u、v在E内任一点可微，且满足C-R条件。

第二章　复变函数和积分

复变函数积分

柯西积分

解析函数与调和函数的关系

线积分与路径无关等价于该函数沿单连域中任何闭曲线的积分为零。

柯西积分定理：单连域内解析积分为零。

如果函数f(z)在单连域E内解析，那么积分　只与起点与终点有关，与连接点和终点的路径无关。

由于复变函数的积分为沿着有向曲线的积分，可以通过二元函数关于坐标的曲线积分式来获得。

若已知曲线的参数方程，则复变函数可以化为定积分计算，这时只要将被积函数f(z)的变量z换为z(t)=x(t)+iy(t),将dz换为　z'(t)dt即可。

对于解析函数的积分，由于积分与路径无关，可以通过与牛顿莱布尼兹公式相同来计算。

至于计算沿封闭路线的积分，往往以柯西积分定理、复合闭路定理、闭路变形公式、柯西积分公式、高阶导数公式为工具。

满足拉普拉斯方程，且具有二阶连续偏导的函数称为调和函数。

任何一个在区域E上解析的函数f(z)=u(x,y)+iv(x,y),其实部与虚部都是该区域上的调和函数。

如果u(x,y)是区域E内的调和函数，则存在一个v(x,y)使u+iv在E内解析。

第三章　级数

一个函数的解析性与该函数能否级数展开是等价的。

罗朗级数

对于一般复数列的讨论可以归结为对两个实数列的讨论。

对于一般复数项级数的讨论可以归结为对实数项级数的讨论。

复变函数项级数：f1(z)+f2(z)+....+fn(z)+...

幂级数是一种特殊复变函数项级数。以cn(z-z0)n为一般项。

幂级数与解析函数有密切关系：

幂级数在一定区域内收敛于一个解析函数

一个解析函数在其解析点的领域内能展开成幂级数。

阿贝尔定理　　收敛圆和收敛半径

达朗贝尔公式

柯西公式

在收敛圆内，幂级数和和函数是解析函数。即，任何一个收敛半径大于零的幂级数在其收敛圆内代表一个解析函数。

泰勒定理　　能展成幂级数

f(z)在区域E内解析的充要条件是　f(z)　在E内任一点z0的领域内可以马尔代展成(z-z0)的幂级数，即泰勒级数。

如果z=z0是f(z)的奇点，那么在奇点的领域内就不能展开成泰勒级数。

罗朗级数

第四章　留数理论

孤立奇点的分类和性质

留数的求法

用留数定理计算实函数积分和无穷限广义积分

如果f(z)在　z0点去心领域内解析，而z0点不解析，称z0为f(z)的孤立奇点。

如果f(z)在z0点的主要部分全部等于零，称z0为f(z)的可去奇点

如果f(z)在z0点的主要部分只有有限项m,　称z0为f(z)的m级极点。

如果f(z)在z0点的主要部分有无穷多项，称z0为f(z)的本性奇点。

可去奇点判定　如果z0为f(z)的孤立奇点，下列三个条件是等价的：

f(z)在z0点的主要部分为零。

limf(z)存在。

f(z)　在点z0的某去心领域有界

m级极点的判定　如果z0为f(z)的孤立奇点，下列三个条件等价：

f(z)在z0点的主要部分为

f(z)在点z0的某去心领域内能表示成

g(z)=1/f(z)以z0　为m级零点

留数定理　把沿封闭曲线积分的整体问题，化为计算其各孤立奇点处留数的局部问题。

留数求法

可去奇点：若z0为f(z)的可去，面积分Res{f(z),z0}=0.

极点：

本性奇点：通过罗朗展开式来求留数。

第五章　保角映射

映射的旋转角不变性　解析函数的导数幅角的几何意义。

映射的保角性　映射具有保持两曲线间夹角的大小与方向不变的特性。　

伸缩率的不变性　当z0取定后，伸缩率|f'(z0)|是确定的，从而与过点z0的曲线C的选择无关。　

保角映射　设w=f(z)在z0的领域内有定义，若映射　w=f(z)在点z0　有保角性（大小、方向不变）和伸缩率不变性，称映射w在点z0是保角的，或w=f(z)在z0处是保角映射。

若　w=f(z)在区域E内解析，则它在E内导数不为零的点处是保角的。

上述保角映射不仅保持曲线夹角的大小不变而且夹角的方向不变。仅保持夹角的绝对值不变而方向相反的映射称为第二类保角映射。

分式线性映射　

任何一个分式线性映射可由两种典型的映射复合而成。

分式线性映射在扩充的复平面上是一一对应的，具有保圆性的保角映射。

这里的保圆性是指：在分式线性映射下，将圆周（直线）映射成圆周（直线）。

也就是说，如果给定的圆周或直线上没有点映射或者无穷远点，那么它就映射成半径为有限的圆周，如果有一点映射成无穷远点，那么它就映射成直线。

分式线性映射除了保圆性之外，还有保对称性。

三种重要的分式线性映射：上半平面映射上半平面，上半平面映射单位圆域，单位圆域映射成单位圆域。